Competition with a .505 Gibbs?? Large diameter bullet holes will cover more area and might get into the next higher scoring ring where a tiny .30 caliber bullet would not. A ..60 caliber might boost an X count better. Hate to shoot a string of 20, prone with that monster. Any chrony data with various loads??
With my .375-.338 felt recoil is completely dependent on velocity with same bullet as powder capacities only vary 6% and I see no reason why powder gas velocities should have much difference as pressures are similar. The rifle eats up a max of 72.5 grains of H4350 and max of 68.0 grains of IMR 4064 with 270 Speer, can't feel the difference, but with 235 grain bullets and a minimum load of 4064 like 67 grains recoil is much like a .300WM.
The 270 Speer btsp, at 2650 has a trajectory much like a .308W with 168's. I managed to hit a 1/2 gallon size rodent (rockchuck, apex rodent of western USA) with it at 250 yards using a tripod but the effects on the rodent were not as spectacular as the .20 P shooting a 40 grain at 3650.
The calculation provided by academy claims to be momentum, P=M*V, but academy gets into some involved calculation similar to that of kinetic energy. For a 180 grain bullet at 3000 fps from a 10 pound rifle academy comes up with 359.65 ft-pounds, good for a visit to your friendly orthopedic medic. Sounds screwy with a peculiar convoluted method.
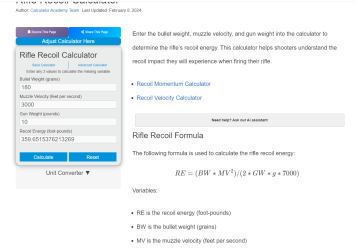
The calculation by shooters calculator for a 10 pound .300WM, comes up with 12.36 fps rifle velocity & 23.73 foot pounds of momentum. My spread sheet came up with 12.543 fps rifle velocity & 24.46 ft pounds of momentum. Recoil impulse is provided in pound seconds, I got to,put that in my spread sheet.
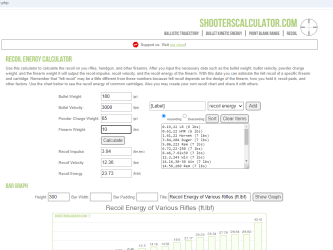
Bison comes up with 24.6 ft-pounds to my 24.46. Then it gets into a kinetic energy calculation
, like 1/2 M*V squared. For a 10 pound rifle, KE = (10/32 * (12.36*12.36))/2 = 23.67 ft-pounds. 10 pounds = .31 slugs, acceleration of gravity 32 fps ps. KE = (.31 * 152.7)/2 = 23.66 ft-pounds. Bison calculator comes up with 24.6 ft-pounds, my spread sheet showed 24.46 ft-pounds of momentum. Bison shows conservation of momentum then gets into kinetic energy like 1/2 M* V squared - this method would come up with 23.67 ft-pounds. Bison puts powder gas velocity at 1.5 times more than bullet velocity, like 3000 * 1.5 = 4500 fps, I used 5200 fps.
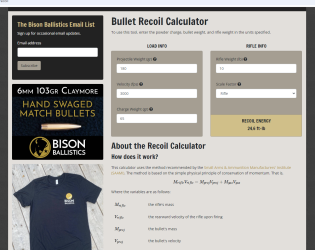
Robinette comes up with 29.78 ft-pounds of recoil , what is "
2g" divided into ( gun vel ^2 * gun weight) ?. Gas velocity effects provided but actual gas velocity not provided. Indications of momentum as effects of bullet velocity should rifle be suspended vs slamming into person's body. Powder gas velocity for Robinett is 1.7 times bullet velocity or 1.7*3000 = 5100 fps, I used 5200 fps. Good discussion & great graphs of m brakes.
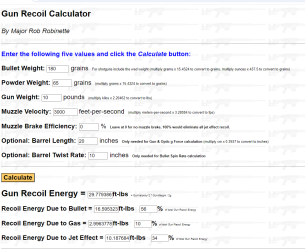
Feel free to copy my spread sheet, it allows multiple same screen comparisons of various combos, simple momentum calculation P=M*V, can be easily run on excel. rifle velocity calculations shown on top of spread sheet.Powder gas velocities can be easily changed. My numbers are real close to those produced by the calculators.
Here is another recoil calculation
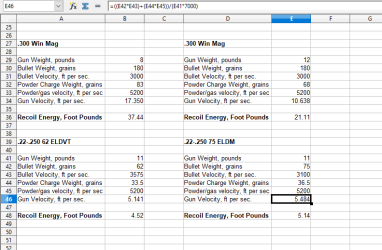
Loads with different burn rate powders having equal velocities don't have much differences in felt recoil but the loads having less powder have slightly less calculated recoil as a result of the powder weight times powder velocity calculation, jet effect described by Robinette. Loading to max pressures with suitable powders there would likely be less than 12% difference in weight between both; this would be reflected by the momentum calculation. The dwell time for bullet acceleration inside the barrel is 1.0 to 1.5 milliseconds for slow & fast burning powder and I cannot feel any difference, 1 to 1.5 milliseconds is real short.
Objective - based on facts & data
Subjective - based on feelings, that hard steel stock butt plate don't feel good.






